HyperLogLog and Beyond (On distinct counting from a data sketching researcher)
HyperLogLog is one of the most useful and elegant algorithms in modern data processing. It counts the distinct items in a data set using tiny space. How tiny? Counting billions of distinct items with 1% error takes 6 KB. That’s an over 1,000,000x reduction in space compared to an exact method!
This post takes a look at HyperLogLog (HLL) and other distinct counting sketches from a researcher’s perspective. Even if you’ve read other blogs or papers on HLL, this post should provide a deeper (and more correct) understanding of the sketch and the underlying statistical processes. It will also look at practical tradeoffs that may make other distinct counting sketches more suitable and dive into some recent developments.
Randomized data sketching: Making Big Data small
HyperLogLog and approximate distinct counting are one problem and solution in a broader topic of data sketching. Data sketching exploits that, in many cases, a dataset is used to answer a limited number of important questions. By storing just the information needed to answer these questions, you can greatly reduce the cost of storing and processing the data.
Beyond distinct counting, some particularly important problems include identifying heavy-hitters in a data stream, testing set membership, and computing quantiles. In each of these cases, computing the exact answer for each of these requires storing all of the data and expensive operations like (partial) sorting. For many of these, computing even a deterministic approximation requires space linear in the size of the data.
Perhaps surprisingly, where deterministic algorithms fail, randomized algorithms succeed. Randomized data sketching methods allow us to solve some of these problems with space that does not depend on the size of the data (like HLL) or grows sublinearly. Instead the size depends on the amount of approximation error.
Designing these algorithms consists of two parts: 1) figuring out a way to represent a data stream with a small random sketch and 2) figuring out how to extract the answer from the sketch. We’ll look at the mechanisms for each of these for HLL.
Hash-based (Coordinated) sampling: The de-duping mechanism
At the core of every distinct counting sketch is the ability to identify and ignore duplicate items. Since not every item can be stored, the sketch consists of a sample of items. The question is how this sample should be represented.
HyperLogLog and essentially all other sketches use hash based sampling. Each item is hashed to a smaller number of bits using a random hash function. It is counted if it does not “collide” with a previous item’s hash. In the case of HLL, an item is hashed to a bin and value.
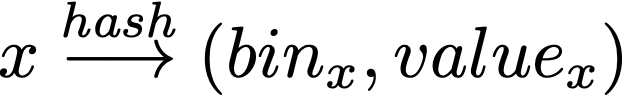
Unlike set membership sketches like the Bloom filter, a distinct counting sketch does not try to store all items inserted into the sketch, thus keeping its size small. For HLL, only the largest value in each bin is kept, so the total size of the sample is the number of bins in the sketch. At the same time, duplicate items cannot affect the sketch since a duplicate cannot increase the value in the bin.
Quantization: Making HLL tiny
While hash based sampling controls the number of bins, the reason that HLL is so efficient compared to other distinct counting sketches is that it further makes the size of each bin tiny.
To generate a hash value, x is first uniformly hashed to 64 bits and the number of leading 0’s in the hash determines the value. Equivalently, x is hashed to a Geometric(1/2) random value. The beauty of this procedure is that it ensures each bin takes very few bits, on the order of log log n where n is the cardinality. To exceed a 5 bit bin’s capacity and get a bin value > 2⁵-1, you expect to have >2³¹ items hashed to each bin. With 1000 bins taking 5 bits each, you can count cardinalities on the order of 2⁴⁰ or 1 trillion.
Estimation:
Let’s first consider a real life scenario that mimics the estimation procedure for a simplified HLL sketch.
Suppose you go on a hike and look for wildlife. After 1 mile, you find that, on average, you hike 0.1 miles before seeing some wildlife. How many wildlife encounters do you expect after hiking 10 miles?
Most people would say 10/0.1 = 100 times (assuming wildlife is uniformly distributed). This illustrates how you’d estimate the total count using just a sample of the encounters. The estimate is N ≈ m/𝔼 D where m is the total distance and D is the distance between encounters.
To see how this maps to a simplified HLL, suppose the hash value for each item is distributed Uniform(0,1) and you take the min in each bin rather than max. The value in each bin represents the distance until you walk before encountering “wildlife,” i.e. a hash value. If you have 10 bins to represent 10 miles and the average value in the bins is 0.1, then you’d estimate that there are 100 distinct items.
Now how does this relate to the (rather mysterious looking) HLL estimator?
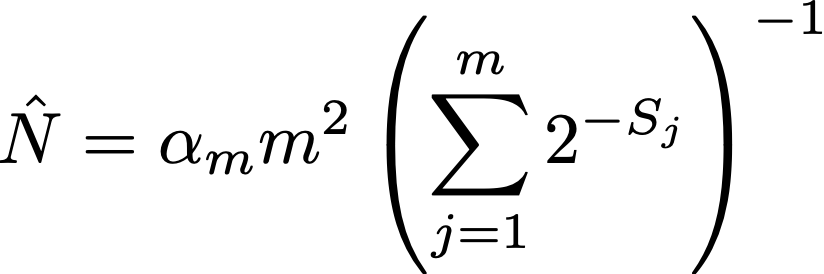
where Sⱼ is the value of the jth bin in sketch S.
The Geometric(1/2) values for HLL arise from discretizing the uniform(0,1) values. Take the -log base 2 of a uniform(0,1) value and round up. Reversing this process by taking 2^(-Sⱼ) gives a discrete approximation Cⱼ to the original uniform(0,1) value. It then becomes clear that the HLL estimator is exactly the same as that for our wildlife estimate except for a correction factor α_m to handle the discretization.
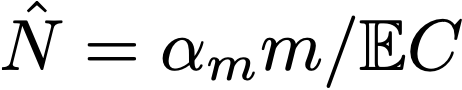
Vs Coin flipping:
The way HLL has often been described is as counting using “coin flipping,” and indeed the Geometric(1/2) random variables in HLL do correspond to coin flips. While this provides intuition why information about the cardinality is stored in the sketch, from the simple continuous version of HLL with no coin flipping, you can see that coin flipping has nothing to do with how HLL really works. In fact, if you did take the coin flipping perspective and average together cardinality estimates from each bin, you’ll find that your estimates had infinite variance and the resulting cardinality estimate is worthless!
What’s really interesting about the continuous to discrete viewpoint is that this motivates why the HLL cardinality estimator is not just very good, but nearly optimal because, in the continuous case, the estimator is asymptotically optimal with optimal constant factors!
So hopefully now you understand the basic ideas that make HLL tick: hashing to deduplicate, sampling and quantization to control size, and good estimation to extract the cardinality. For the most part, implementations of HLL almost exactly follow the original algorithm described in 2007, at least for large cardinalities.
But is this the best you can do?
Improvements:
Although HLL has virtually become a de facto standard for cardinality estimation, it is actually suboptimal in a few ways. Here we will go over meaningful improvements to HLL that make it closer to truly optimal.
Infinite cardinalities: Dropping LogLog with an offset
The first improvement is the use of offsets and 4 bit bins. Rather than directly storing bin values, the sketch stores the minimum value over all bins as a baseline. Each bin then stores offsets from the baseline. This ensures almost all bins only need 4 bits while the few exceptional bins can be handled separately. Both Presto and Druid, where this first appeared [1] as well as Apache Dataksketches, provide these 4 bit bins with offsets.
Interestingly, this almost yields a sketch with optimal space complexity, the log log n dependence goes away and HyperLogLog should actually be called HyperConstant (though this is not proven anywhere that I am aware of)! Although this idea was first introduced in the theoretical paper “An Optimal Algorithm for the Distinct Elements Problem” by Kane, Nelson, and Woodruff, that sketch is impractical due to bad constant factors.
(Technically, using the min for a baseline may not yield optimal space complexity, but any quantile, e.g. the 0.0001th, should. This can be proven using a variation of the self-similar sketch idea in my 2014 KDD paper [4]. )
Handling small cardinalities:
A second meaningful change improves counting for small and medium cardinalities. Heule et al (2013) “HyperLogLog in Practice” noticed that HLL was biased for medium cardinalities with gross overestimates of the error. They provided a way to empirically correct these for a few sketch sizes. Ting (2019) “Approximate Distinct Counts for Billions of Datasets” showed how to do this analytically for any sketch size using a composite marginal likelihood. Ertl (2017) gives a simple estimator that is easier to implement nearly as good for getting estimates (but not errors).
Also, when cardinalities are very small, storing the raw hash values takes less space than instantiating a full array of bins. This is particularly useful in Group By queries with many groups, many of which only contain a few items. Both Google’s HLL++ and Apache Datasketches implement these two improvements.
Streaming:
When the data arrives as a single stream and sketches do not need to be merged, the HIP (also known as the martingale) [3,4] estimator is provably the optimal estimator for any distinct counting sketch. It reduces the variance, and hence the space required to achieve a desired error guarantee, by a factor of 1.57 when compared to the original HLL estimator.
When sketches do need to be merged, it is technically still possible to exploit the streaming estimates. In this paper [6], I show how to do this for MinCount/Bottom-k sketches. It should be relatively easy to adapt the simple estimator to HLL. In fact, part of the work is already done by Ertl below.
Set operations:
Given two HLL sketches on data sets X and Y, taking their bin-wise max produces another HLL sketch on the union X ∪ Y. This mergeability property is a key to practical use of HLL. It enables building distinct counting data cubes. However, using unions to compute other quantities like set intersections through the inclusion-exclusion rule leads to terrible estimates. Ertl (2017) shows how a maximum likelihood estimation can yield better intersection and set difference estimates.
Smaller representations:
There have been several works further improving the space efficiency of HLL beyond that achieved with 4 bit bins.
A related topic: Privacy
Distinct counting sketches also have important connections to data privacy. In fact, HLL provides inherent differential privacy guarantees when the cardinalities are large enough and the hash function is not shared. Roughly, this means that it is “safe” to release HLL sketches to the public, since they preserve the privacy of the people that they count.
Beyond data release, HLL and distinct counting sketches are also useful for identifying potential data privacy violations.
Conclusion
Hopefully, this has provided some interesting, deeper insight into how distinct counting sketches work and new developments in the area. And for those that need distinct counting sketches, look at sketches beyond HLL — other sketches may be better for your use cases.
[1] Ertl, Otmar (2017). New cardinality estimation algorithms for HyperLogLog sketches. Arxiv
[2] Cohen, E. (2014). All-distances sketches, revisited: HIP estimators for massive graphs analysis. PODS
[3] Ting, D. (2014). Streamed approximate counting of distinct elements. KDD.
[4] Ting, D. (2016) “Towards Optimal Cardinality estimation of Unions and Intersections with Sketches”. KDD
[5] Heule, S., Nunkesser, M., and Hall, A. (2013). HyperLogLog in Practice: Algorithmic Engineering of a State of The Art Cardinality Estimation Algorithm. EDBT.
[6] https://datasketches.apache.org/docs/Theta/ThetaSketchFramework.html
[7] Anirban Dasgupta , Kevin J. Lang, Lee Rhodes, Justin Thaler (2016). A Framework for Estimating Stream Expression Cardinalities. ICDT
[8] Pettie, S. Wang, D. (2021) Information Theoretic Limits of Cardinality Estimation: Fisher Meets Shannon. STOC.